8. Properties of Curves

d. Arc Length, Arc Length Parameter, and Speed

1. Arc Length of a Curve

To find a formula for the length of a parametric curve, r⃗(t)\vec{r}(t), from A=r⃗(a)A=\vec{r}(a) to B=r⃗(b)B=\vec{r}(b), we approximate the curve by straight line segments and sum the lengths of the segments. In the limit, as we use more segments which are shorter and shorter, this turns into an integral for the exact length of the curve.

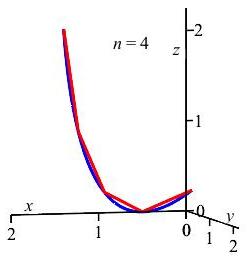
We start by dividing the curve, r⃗(t)=(x(t),y(t))\vec r(t)=(x(t),y(t)), into nn segments by partitioning the tt values at t0,t1,⋯,ti−1,ti,⋯,tnt_0,t_1,\cdots,t_{i-1},t_{i},\cdots,t_{n}. As a shorthand, we define: xi=x(ti),yi=y(ti),zi=z(ti) x_i=x(t_i), \qquad y_i=y(t_i), \qquad z_i=z(t_i) We use the distance formula in three dimensions to determine the length of each of the straight line segments from r⃗(ti−1)\vec{r}\left(t_{i-1}\right) to r⃗(ti)\vec{r}\left(t_{i}\right). Finally, we sum these straight line differences from i=1i=1 to i=ni=n to get an approximation to the length of the curve: L≈∑i=1n(xi−xi−1)2+(yi−yi−1)2+(zi−zi−1)2 L\approx\sum_{i=1}^n \sqrt{\left(x_i-x_{i-1}\right)^2+ \left(y_i-y_{i-1}\right)^2+\left(z_i-z_{i-1}\right)^2} In the plot, a curve, shown in blue, is partitioned into 44 approximating line segments, in red. The length of the blue curve is approximated by summing the lengths of the red line segments.

eg_arclength_n4

Next we note that xi−xi−1=Δx=ΔxΔtΔtx_i-x_{i-1}=\Delta x=\dfrac{\Delta x}{\Delta t}\Delta t. The same holds true for the yy and zz differences. Substituting these into the previous equation, we get L≈∑i=1nΔx2+Δy2+Δz2≈∑i=1n(ΔxΔtΔt)2+(ΔyΔtΔt)2+(ΔzΔtΔt)2≈∑i=1n(ΔxΔt)2+(ΔyΔt)2+(ΔzΔt)2Δt\begin{aligned} L&\approx\sum_{i=1}^n \sqrt{\Delta x^2+\Delta y^2+\Delta z^2} \\ &\approx\sum_{i=1}^n \sqrt{ \left(\dfrac{\Delta x}{\Delta t}\Delta t\right)^2 +\left(\dfrac{\Delta y}{\Delta t}\Delta t\right)^2 +\left(\dfrac{\Delta z}{\Delta t}\Delta t\right)^2} \\ &\approx\sum_{i=1}^n \sqrt{ \left(\dfrac{\Delta x}{\Delta t}\right)^2 +\left(\dfrac{\Delta y}{\Delta t}\right)^2 +\left(\dfrac{\Delta z}{\Delta t}\right)^2}\,\Delta t \end{aligned}

This approximation becomes exact in the limit as the number of segments nn becomes infinite and Δt\Delta t goes to 00, as shown in the animation. At the same time the quotient ΔxΔt\dfrac{\Delta x}{\Delta t} approaches the derivative dxdt\dfrac{dx}{dt}. Thus, the limit of the sum becomes the integral: L=lim⁡Δt⟶0∑i=1n(ΔxΔt)2+(ΔyΔt)2+(ΔzΔt)2Δt=∫ab(dxdt)2+(dydt)2+(dzdt)2dt\begin{aligned} L&=\lim_{\Delta t\longrightarrow 0} \sum_{i=1}^n \sqrt{ \left(\dfrac{\Delta x}{\Delta t}\right)^2 +\left(\dfrac{\Delta y}{\Delta t}\right)^2 +\left(\dfrac{\Delta z}{\Delta t}\right)^2}\,\Delta t \\ &=\int_a^b \sqrt{\left(\dfrac{dx}{dt}\right)^2 +\left(\dfrac{dy}{dt}\right)^2 +\left(\dfrac{dz}{dt}\right)^2}\,dt \end{aligned}

Notice that the square root in this formula is just the length of the velocity. So L=∫ab∣v⃗∣dt L=\int_a^b |\vec{v}|\,dt

Arc Length Differential and Formulas for the Arc Length

Arc Length Differential and Arc Length Integral
The (Scalar) Differential of Arc Length is the differential: ds=dx2+dy2+dz2=(dxdt)2+(dydt)2+(dzdt)2dt=∣v⃗∣dt\begin{aligned} ds&=\sqrt{dx^2+dy^2+dz^2} \\ &=\sqrt{\left(\dfrac{dx}{dt}\right)^2 +\left(\dfrac{dy}{dt}\right)^2 +\left(\dfrac{dz}{dt}\right)^2}\,dt=|\vec{v}|\,dt \end{aligned} If a curve runs between the points AA and BB, then the Arc Length of the Curve is the integral: L=∫ABds=∫ABdx2+dy2+dz2 L=\int_A^B\,ds=\int_A^B \sqrt{dx^2+dy^2+dz^2} where the endpoints AA and BB are the limits on the integral. If we specify a parametrization (since there could be more than one way to parametrize the curve) as r⃗(t)\vec{r}(t), then the endpoints are A=r⃗(a)A=\vec{r}(a) and B=r⃗(b)B=\vec{r}(b) and we write: L=∫ab∣v⃗∣dt L=\int_a^b |\vec{v}|\,dt where the limits on the integral are the values of tt at AA and BB.

Compute the arclength of the twisted cubic r⃗(t)=(t,t2,23t3)\vec{r}(t)=\left(t,t^2,\dfrac{2}{3}t^3\right) between t=0t=0 and t=3t=3.

The velocity is v⃗=(1,2t,2t2)\vec{v}=(1,2t,2t^2) and its length is ∣v⃗∣=1+4t2+4t4=(1+2t2)2=1+2t2. |\vec{v}|=\sqrt{1+4t^2+4t^{4}} =\sqrt{(1+2t^2)^2}=1+2t^2. So its arc length is L=∫(0,0,0)(3,9,18)ds=∫03∣v⃗∣dt=∫03(1+2t2)dt=[t+23t3]03=3+18=21\begin{aligned} L&=\int_{(0,0,0)}^{(3,9,18)}ds =\int_0^3 |\vec{v}|\,dt =\int_0^3 (1+2t^2)\,dt \\ &=\left[t+\dfrac{2}{3}t^3\right]_0^3=3+18=21 \end{aligned}

Compute the circumference of the circle r⃗(θ)=(Rcos⁡(θ),Rsin⁡(θ),3)\vec{r}(\theta)=(R\cos(\theta),R\sin(\theta),3).

Answer

L=2πRL=2\pi R

[×]

Solution

The circumference of a circle is the arc length of 11 revolution, from θ=0\theta=0 to θ=2π\theta=2\pi. So the circumference is L=∫02π∣v⃗∣dθ L=\int_0^{2\pi} |\vec{v}|\,d\theta To compute this, we need the magnitude of the velocity vector, which is ∣v⃗∣=(dxdθ)2+(dydθ)2+(dzdθ)2=(−Rsin⁡θ)2+(Rcos⁡θ)2+02=R2(sin⁡2θ+cos⁡2θ)=R\begin{aligned} |\vec{v}| &=\sqrt{\left(\dfrac{dx}{d\theta}\right)^2 +\left(\dfrac{dy}{d\theta}\right)^2 +\left(\dfrac{dz}{d\theta}\right)^2} \\ &=\sqrt{(-R\sin\theta)^2+(R\cos\theta)^2+0^2} \\ &=\sqrt{R^2(\sin^2\theta+\cos^2\theta)}=R \end{aligned} So the circumference is L=∫02π∣v⃗∣dθ=∫02πRdθ=2πR\begin{aligned} L=\int_0^{2\pi} |\vec{v}|\,d\theta =\int_0^{2\pi} R\,d\theta =2\pi R \end{aligned}

gg 

[×]

Check

Notice that L=2πRL=2\pi R is the formula you already know for the circumference of a circle. In fact, this is one way that formula is derived!

[×]

If the parameter happens to be zz, while xx and yy are functions of zz:   x=x(z)x=x(z) and y=y(z)y=y(z),   then the arc length differential becomes ds=(dxdz)2+(dydz)2+1dz ds=\sqrt{\left(\dfrac{dx}{dz}\right)^2+\left(\dfrac{dy}{dz}\right)^2+1}\,dz and the arc length integral is: L=∫abds=∫ab(dxdz)2+(dydz)2+1dz L=\int_a^b\,ds=\int_a^b \sqrt{\left(\dfrac{dx}{dz}\right)^2+\left(\dfrac{dy}{dz}\right)^2+1}\,dz where aa and bb are now the values of zz at the endpoints. Similar formulas hold when the parameter is xx or yy.

Compute the arclength of the helix   x=4cos⁡(13z),y=4sin⁡(13z)x=4\cos\left(\dfrac{1}{3}z\right), y=4\sin\left(\dfrac{1}{3}z\right)   between z=0z=0 and z=18πz=18\pi.

Answer

L=30πL=30\pi

[×]

Solution

The arc length is L=∫ab(dxdz)2+(dydz)2+1dz=∫018π169sin⁡2(13z)+169cos⁡2(13z)+1dz=∫018π169+1dz=[53z]018π=30π\begin{aligned} L&=\int_a^b \sqrt{\left(\dfrac{dx}{dz}\right)^2 +\left(\dfrac{dy}{dz}\right)^2+1}\,dz \\ &=\int_0^{18\pi} \sqrt{\dfrac{16}{9}\sin^2\left(\dfrac{1}{3}z\right) +\dfrac{16}{9}\cos^2\left(\dfrac{1}{3}z\right)+1}dz \\ &=\int_0^{18\pi} \sqrt{\dfrac{16}{9}+1}dz =\left[\dfrac{5}{3}z\right]_0^{18\pi}=30\pi \end{aligned}

[×]

Notice this is the same as the helix parametrized as r⃗(θ)=(4cos⁡θ,4sin⁡θ,3θ)\vec{r}(\theta)=(4\cos\theta,4\sin\theta,3\theta) for 0≤θ≤6π0 \le \theta \le 6\pi.

You can also practice computing the arc length of curves using the following two Maplets (requires Maple on the computer where this is executed):

Arc Length in 2D   Rate It

Arc Length in 3D   Rate It

© 2025 MYMathApps

Supported in part by NSF Grant #1123255